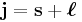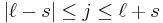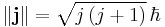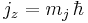Total angular momentum quantum number

Further information: Azimuthal quantum number#Addition of quantized angular momenta

In quantum mechanics, the total angular quantum momentum numbers parameterize the total angular momentum of a given particle, by combining its orbital angular momentum and its intrinsic angular momentum (i.e., its spin).

If s is the particle's spin angular momentum and ℓ its orbital angular momentum vector, the total angular momentum j is

$\mathbf j = \mathbf s %2B \boldsymbol {\ell}$

The associated quantum number is the main total angular momentum quantum number j. It can take the following range of values, jumping only in integer steps:

$|\ell - s| \le j \le \ell %2B s$

where ℓ is the azimuthal quantum number (parameterizing the orbital angular momentum) and s is the spin quantum number (parameterizing the spin).

The relation between the total angular momentum vector j and the total angular momentum quantum number j is given by the usual relation (see angular momentum quantum number)

$\Vert \mathbf j \Vert = \sqrt{j \, (j%2B1)} \, \hbar$

the vector's z-projection is given by

$j_z = m_j \, \hbar$

where m_j is the secondary total angular momentum quantum number. It ranges from −j to +j in steps of one. This generates 2j + 1 different values of m_j.

The total angular momentum corresponds to the Casimir invariant of the Lie algebra so(3) of the three-dimensional rotation group.

References

Griffiths, David J. (2004). Introduction to Quantum Mechanics (2nd ed.). Prentice Hall. ISBN 0-13-805326-X.

Total angular momentum quantum number

See also

References

External links